 376
/
376
/

标签: 数学 哲学 芝诺悖论
(PS:七年之后再看这篇小论文,我也不知道自己当初写的是什么玩意。。。)
摘要:数学对哲学有着重大影响。这种影响不仅表现在有些哲学观点直接以数学成就为基础,更重要的是数学的思维和方法深刻影响着哲学问题的论证,包括正反两面。芝诺悖论就是其中一个经典例子,它揭示出了关于有限与无限、连续性与间断性的矛盾,不断受到关注。本文则试图通过所学的极限和概率的内容并结合前人的研究对其作出回应。
关键字:数学;哲学;极限;概率
自古以来,数学对哲学的影响之大是不言而喻的。在古希腊,各门学科尚未独立,所有学问都被统称为哲学,数学也不例外。伟大的数学家毕达戈拉斯本身就是一个哲学家。他以数为万物之本原,强调世界的和谐之美。数的抽象性使哲学得以跳出具象思维,逐渐形成其理性主义传统,这就大大提升了哲学的思辨水平,极大地促进了后来哲学的发展。以《几何原本》为代表,数学演绎推理的严密性和确定性,正是哲学家所梦寐以求的。就如柏拉图,他显然也是深受这种观念的影响,据说在他的学园门口写着:“不懂几何学者禁止入内。”乃至现代,罗素也是兼通数学与哲学,而且两方面都取得了巨大成就。
然而,这种借助数学有时也会给哲学带来大“麻烦”。毕达戈拉斯学派通过对数的研究,在数目中间发现各种和谐的特性和比例,于是他们就以数为万物本原,视世界为一和谐的整体,以此来回答世界的本原和世界的规律性问题。但无理数的发现,使得这一哲学观点的基础崩塌了,可谓是成于斯亦败于斯。当然,这样直接以数学成就为基础的哲学观点不多,但引入数学分析或借助数学思维来论证的情况则有不少,其中一个经典例子便是“芝诺悖论”。
芝诺悖论主要是为了论证其师巴门尼德的哲学观点。巴门尼德是形而上学的奠基人,他认为存在是一、是不动的。这种观点显然是高度抽象、难以理解的。芝诺便系统地运用归谬法,通过否定由感官观察到的多和运动这两种现象,来反证其师的观点。这些论证看起来逻辑严密、无懈可击,但又与常识和经验观察相互矛盾,显得很荒谬,故而被称为悖论。芝诺悖论有一系列论证,其中“阿基里斯追不上乌龟”和“飞矢不动”论证尤为经典,二者也是比较常见的两个悖论。
在“阿基里斯追不上乌龟”论证中,阿基里斯是古希腊的跑步健将,在常识经验中,阿基里斯肯定能够追得上乌龟。但芝诺的论证是,阿基里斯要追上乌龟,就得先到达乌龟的出发点,但此时乌龟又已向前行进了一段距离,阿基里斯又得继续向前,再到达新的出发点,如此重复不断,有着无数个新的出发点。因此,乌龟尽管速度很慢,但总会向前爬行一段距离;阿基里斯尽管速度比乌龟快,但只是在追赶不断出现的新的出发点,阿基里斯只能无限接近而永远都无法追上乌龟。归结起来就是无法在有限时间内完成超过无限个点的动作。
“飞矢不动”论证则是,每一物体在占据与自身相等的空间并且不越出这个空间时都是静止的,飞行的箭在一定时间里要经过许多个点,在每一瞬间,箭都处在某个点上,只占据着与自身相等的空间,因而是在该点上飞箭是静止的,进而由所有静止的点集合起来也仍然是静止的,所以箭是不动的。
可以看出,这两个论证涉及到了数学上有限与无限、连续性与间断性(离散性)的问题,而不仅仅是芝诺的诡辩。正因为如此,芝诺悖论并没有随着时间的流逝而被人遗忘,反而不断受到关注,许多人提出各种办法并自认为解决了芝诺悖论,既包括哲学家,也包括逻辑学家,当然其中也少不了数学家。芝诺悖论力图否认运动的真实性,正如学者们指出的,“芝诺论辩的全部要害在于用运动轨迹代替运动本身。许多现代分析哲学家进一步指出,芝诺用数学化的运动轨迹代替物理的运动轨迹,就将真实的物理运动导入关于无限的数学迷途之中。”[1]简而言之,哲学问题被数学化了。解铃还需系铃人,下面我们将试图用数学方法作出反驳。
对于“阿基里斯追不上乌龟”的悖论,如果用初等数学来解决,那么似乎显得很简单。我们已知阿基里斯的速度 和乌龟的速度
和乌龟的速度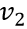 以及开始时乌龟领先阿基里斯的距离d,那么假设阿基里斯在 t 时追上乌龟,则有
以及开始时乌龟领先阿基里斯的距离d,那么假设阿基里斯在 t 时追上乌龟,则有

于是可以得到:

 的时间后追上乌龟。但是,我们是已经预先假设阿基里斯能够追上乌龟才算出时间的,这是从结果逆推过程;而芝诺的论证中并没有这个假设,他是直接从过程推出结论。这也就是说我们和芝诺的逻辑出发点及逻辑演绎方式是不同的,我们的计算最多只能说明从同样的条件出发,运用不同的逻辑可以得出相反的结论。有人由此进一步认为“数学所告诉我们的不过是,如果能的话,需要多少时间,但数学不解决‘是否能’的问题。”[2]
的时间后追上乌龟。但是,我们是已经预先假设阿基里斯能够追上乌龟才算出时间的,这是从结果逆推过程;而芝诺的论证中并没有这个假设,他是直接从过程推出结论。这也就是说我们和芝诺的逻辑出发点及逻辑演绎方式是不同的,我们的计算最多只能说明从同样的条件出发,运用不同的逻辑可以得出相反的结论。有人由此进一步认为“数学所告诉我们的不过是,如果能的话,需要多少时间,但数学不解决‘是否能’的问题。”[2]
因此,如果要解决“阿基里斯追不上乌龟”的悖论,就应当从其自身的逻辑出发进行演绎。芝诺的逻辑不是把追赶过程当作一个整体,而是将其分为无限个的分段,并且往后的每一段不断变小,无限趋近于零但又不等于零。这就让我们联想起惠施的名言:“一尺之捶,日取其半,万世不竭。”通过对比发现,芝诺的逻辑恰恰是惠施的分析的逆过程,都体现了极限的观点。如果我们通过逆运算,将芝诺所划分的每一段累加起来,并且结果等于某个常数,也就是说乌龟领先阿基里斯的总距离是确定的,当到达这个距离时,阿基里斯就追上了乌龟,那么芝诺悖论的论证就是错误的。
现在,我们首先计算每一段距离的长度。由于速度保持不变,所以只需计算阿基里斯追赶每一段距离的时间。设共有 n 段距离,每一段的追赶时间为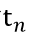 ,于是有
,于是有

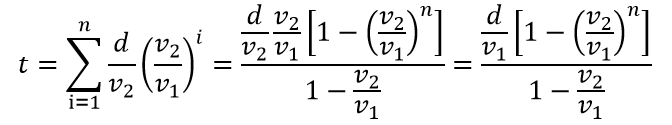
由于阿基里斯的速度 大于乌龟的速度
大于乌龟的速度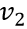 ,即
,即 ,则
,则

即时间的等比数列 收敛到 0
收敛到 0

那么阿基里斯的追赶路程 。这是个确定的值,也是前面用初等数学计算所得的结果:阿基里斯将在经过
。这是个确定的值,也是前面用初等数学计算所得的结果:阿基里斯将在经过 的时间、追赶
的时间、追赶 的路程后追上乌龟。这正符合我们之前的预期,因此“阿基里斯追不上乌龟”的悖论是不成立的。
的路程后追上乌龟。这正符合我们之前的预期,因此“阿基里斯追不上乌龟”的悖论是不成立的。
至于“飞矢不动”悖论,该论证也是对具有连续性的时间进行分割,从而把每一瞬间孤立开来,再将其作离散的点集合起来;于是,每一瞬间的静止状态转化成了整个运动过程的静止状态。对前一个悖论的反驳已经证明,将连续性分割为离散性是可能的;而从微积分的原理可知,对连续性函数的积分其实也是一种和运算。所以,芝诺对飞矢的运动进行分割然后再集合是没有问题的。那么,问题就应当出在对于孤立瞬间的运动的分析上。从物理学可知,要判断物体是否运动,就得观察其是否有位移;而对于孤立瞬间的物体,我们的确无法判断是否有位移。
不过,在随机变量一节中,有一个公共汽车站候车的问题,我们把乘客的候车时间作为一个随机变量。类似地,我们也可以利用随机变量来解决“飞矢不动”悖论。
飞矢在一定时间内要飞过许多点,设其出现在其中某一点为随机变量Y,Y 取值范围是 。飞矢的运动过程可视为连续的,其分布密度函数
。飞矢的运动过程可视为连续的,其分布密度函数 显然是非负可积的,于是存在随机变量 Y 的分布函数
显然是非负可积的,于是存在随机变量 Y 的分布函数 。由分布密度函数的性质4
。由分布密度函数的性质4

这表明,飞矢出现在任一瞬间 a 的概率为0
但是也有许多人指出,“飞矢不动”悖论恰恰否定了时空的连续性,其前提是时空是离散分立的;那么用连续型随机变量来反驳该悖论就是无效的。其实这种观点本身就是有问题的。该悖论中时空之所以是离散的,在于芝诺对时空进行分割,然而前面已经说到,分割后的离散的点是可以重新收敛起来从而构成连续性的。如果芝诺的前提是时空是不连续的,那么这个前提本身就是不成立的。
即使承认芝诺的前提,我们也能得出相同的结论。既然时空是离散的,那么就用离散型随机变量来进行分析。设随机变量 Y 取值为 其概率分布为
其概率分布为 且
且 ,概率之和
,概率之和 。对于飞矢,取其特殊运动情形即匀速直线运动,则飞矢出现在每一点的概率相等。设共有 n 点,则
。对于飞矢,取其特殊运动情形即匀速直线运动,则飞矢出现在每一点的概率相等。设共有 n 点,则 ;由于
;由于 ,于是
,于是

这与之前的结论是一致的。这表明,即使时空是离散的,由于在一定的时空内这些离散点有无限多个,孤立地描述飞矢在某个瞬间的情形也是毫无意义的。
因此,芝诺的“飞矢不动”悖论是不成立的。这里的反驳不是说飞矢在每一瞬间就都是运动的,而是说像芝诺这样孤立考察飞矢在单个瞬间是否运动是毫无意义的,因为我们无法判断物体是否有位移,从而也就无从判断物体是运动还是静止。
总而言之,对于芝诺的“阿基里斯追不上乌龟”悖论,我们通过应用极限的观点发现,连续的有限者可以进行无限地离散分割,反过来也可以重新将分割后的离散者收敛为有限的连续者。芝诺悖论之悖在于运用了前者,却否认了后者。至于“飞矢不动”悖论,通过运用概率的随机变量方法可知,运动物体出现在单个点的概率为零,表明在单个瞬间点上来讨论运动与否问题是没有意义的,既无法判断其运动,也不能判断其静止。
以上对芝诺的两个悖论表述和对其进行反驳的尝试,无论哪一方更有说服力,都说明了数学能够并且确实参与了哲学问题的论证和反驳,鲜明地体现了数学对哲学的影响。绝大部分哲学问题固然不可能直接用数学方法来论证,但数学思维的严密、精确和数学方法工具的巧妙、明白,对哲学思考显然有着重大影响,这非常有利于增强哲学论证的可靠性和严密性。也无怪乎诸如罗素等的许多哲学家本身就是一个伟大的数学家;而反过来,许多数学家也同样在哲学方面有很深的造诣。
参考文献
[1]吴国盛.芝诺悖论今昔谈.哲学动态,1992(12).
[2]罗契,郑伟宏.为芝诺悖论一辩.复旦学报(社会科学版),1982(1).
[3]刘二中. 解析芝诺悖论内含的逻辑漏洞.自然辩证法研究,2005,21(11).
[4]张兴.芝诺悖论的结构.自然辩证法研究,2004,20(11).
[5]亚里士多德.物理学.北京:商务印书馆,1982,190~192.
原创文章,转载请先联系作者。
